wer计算
背景
根据word-error-rate-calculation中提出的计算方法。
初体验
示例
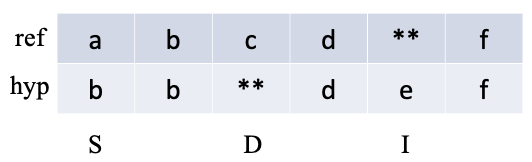
ref(reference)表示标注文本序列,hyp(hypothesis)表示预测文本序列,则可以计算 cer/wer = 3,其中一次替换错误(S),一次删除错误(D),一次插入错误(I)。
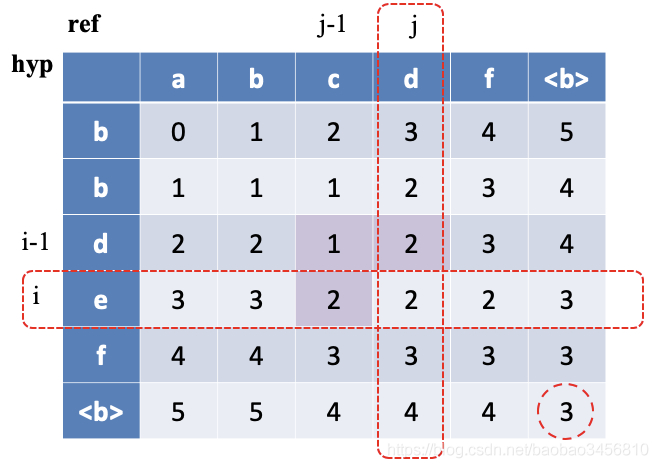

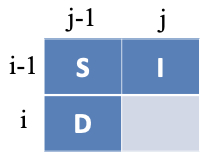
- 时间复杂度:O(m*n)
- 空间复杂度:O(m*n)
代码
import numpy as np
def levenshtein_distance(hypothesis: list, reference: list):
"""编辑距离
计算两个序列的levenshtein distance,可用于计算 WER/CER
参考资料:
https://www.cuelogic.com/blog/the-levenshtein-algorithm
https://martin-thoma.com/word-error-rate-calculation/
C: correct
W: wrong
I: insert
D: delete
S: substitution
:param hypothesis: 预测序列
:param reference: 真实序列
:return: 1: 错误操作,所需要的 S,D,I 操作的次数;
2: ref 与 hyp 的所有对齐下标
3: 返回 C、W、S、D、I 各自的数量
"""
len_hyp = len(hypothesis)
len_ref = len(reference)
cost_matrix = np.zeros((len_hyp + 1, len_ref + 1), dtype=np.int16)
# 记录所有的操作,0-equal;1-insertion;2-deletion;3-substitution
ops_matrix = np.zeros((len_hyp + 1, len_ref + 1), dtype=np.int8)
for i in range(len_hyp + 1):
cost_matrix[i][0] = i
for j in range(len_ref + 1):
cost_matrix[0][j] = j
# 生成 cost 矩阵和 operation矩阵,i:外层hyp,j:内层ref
for i in range(1, len_hyp + 1):
for j in range(1, len_ref + 1):
if hypothesis[i-1] == reference[j-1]:
cost_matrix[i][j] = cost_matrix[i-1][j-1]
else:
substitution = cost_matrix[i-1][j-1] + 1
insertion = cost_matrix[i-1][j] + 1
deletion = cost_matrix[i][j-1] + 1
# compare_val = [insertion, deletion, substitution] # 优先级
compare_val = [substitution, insertion, deletion] # 优先级
min_val = min(compare_val)
operation_idx = compare_val.index(min_val) + 1
cost_matrix[i][j] = min_val
ops_matrix[i][j] = operation_idx
match_idx = [] # 保存 hyp与ref 中所有对齐的元素下标
human_hypothesis = []
human_reference = []
human_eval = []
x = []
i = len_hyp
j = len_ref
nb_map = {"N": len_ref, "C": 0, "W": 0, "I": 0, "D": 0, "S": 0}
while i >= 0 or j >= 0:
i_idx = max(0, i)
j_idx = max(0, j)
if ops_matrix[i_idx][j_idx] == 0: # correct
if i-1 >= 0 and j-1 >= 0:
match_idx.append((j-1, i-1))
nb_map['C'] += 1
human_hypothesis.append(hypothesis[i-1])
human_reference.append(reference[j-1])
human_eval.append(' ')
# 出边界后,这里仍然使用,应为第一行与第一列必然是全零的
i -= 1
j -= 1
# elif ops_matrix[i_idx][j_idx] == 1: # insert
elif ops_matrix[i_idx][j_idx] == 2: # insert
human_hypothesis.append(hypothesis[i-1])
human_reference.append('*')
human_eval.append('I')
i -= 1
nb_map['I'] += 1
# elif ops_matrix[i_idx][j_idx] == 2: # delete
elif ops_matrix[i_idx][j_idx] == 3: # delete
human_hypothesis.append('*')
human_reference.append(reference[j-1])
human_eval.append('D')
j -= 1
nb_map['D'] += 1
# elif ops_matrix[i_idx][j_idx] == 3: # substitute
elif ops_matrix[i_idx][j_idx] == 1: # substitute
human_hypothesis.append(hypothesis[i-1])
human_reference.append(reference[j-1])
human_eval.append('S')
i -= 1
j -= 1
nb_map['S'] += 1
# 出边界处理
if i < 0 and j >= 0:
nb_map['D'] += 1
elif j < 0 and i >= 0:
nb_map['I'] += 1
match_idx.reverse()
human_hypothesis.reverse()
human_reference.reverse()
human_eval.reverse()
wrong_cnt = cost_matrix[len_hyp][len_ref]
nb_map["W"] = wrong_cnt
# print("ref: %s" % " ".join(reference))
# print("hyp: %s" % " ".join(hypothesis))
# print(nb_map)
# print("match_idx: %s" % str(match_idx))
wer = int(nb_map["W"] / nb_map["N"]*100)
# print("REF : %s" % " ".join(human_reference))
# print("HYP : %s" % " ".join(human_hypothesis))
# print("EVAL: %s" % " ".join(human_eval))
# print("WER : {0}%".format(wer))
return [wer, nb_map, human_reference, human_hypothesis, human_eval]
# return wrong_cnt, match_idx, nb_map
if __name__ == '__main__':
hypothesis = ['b', 'e', 'y', 'u', 't']
reference = ['b', 'e', 'a', 'u', 't', 'y']
print(levenshtein_distance(hypothesis, reference))